蓝桥杯2022年B组省赛 —— 个人题解

这篇是后来补发的，过了老久才想起来我的蓝桥杯题解还没发出来，所以这里补一份

试题 A: 排列字母

本题总分：5 分

【问题描述】小蓝要把一个字符串中的字母按其在字母表中的顺序排列。例如，LANQIAO 排列后为 AAILNOQ。又如，GOODGOODSTUDYDAYDAYUP 排列后为 AADDDDDGGOOOOPSTUUYYY 。请问对于以下字符串，排列之后字符串是什么？ WHERETHEREISAWILLTHEREISAWAY
【答案提交】这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个由大写字母组成的字符串，在提交答案时只填写这个字符串，填写多余的内容将无法得分。

1
2
3

# 忘存代码了
print('I forgot to save the code...')

试题 B: 寻找整数

本题总分：5 分

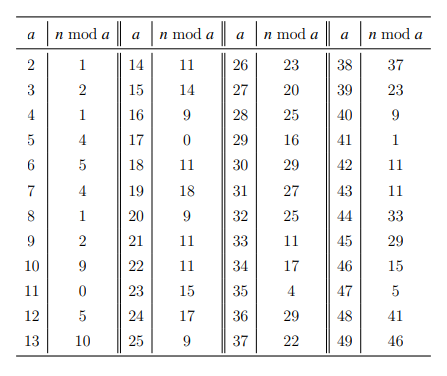
【问题描述】有一个不超过 1017 的正整数 n，知道这个数除以 2 至 49 后的余数如下表所示，求这个正整数最小是多少。
【答案提交】这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

equal = True
result = False
mods = {
    2: 1,
    3: 2,
    4: 1,
    5: 4,
    6: 5,
    7: 4,
    8: 1,
    9: 2,
    10: 9,
    11: 0,
    12: 5,
    13: 10,
    14: 11,
    15: 14,
    16: 9,
    17: 0,
    18: 11,
    19: 18,
    20: 9,
    21: 11,
    22: 11,
    23: 15,
    24: 17,
    25: 9,
    26: 23,
    27: 20,
    28: 25,
    29: 16,
    30: 29,
    31: 27,
    32: 25,
    33: 11,
    34: 17,
    35: 4,
    36: 29,
    37: 22,
    38: 37,
    39: 23,
    40: 9,
    41: 1,
    42: 11,
    43: 11,
    44: 33,
    45: 29,
    46: 15,
    47: 5,
    48: 41,
    49: 46
    }
i = 1
while i <= 10**17:
    i *= 11
    equal = True
    for j in range(2,50):
        if i % j != mods[j]:
            print(f'{i} % {j} = {i%j} != {mods[j]}')
            equal = False
            break
    if equal:
        num = i
        break
if equal: print(f'result: {num}')
else: print('No Result')

试题 C: 纸张尺寸

时间限制：1.0s
内存限制：512.0MB
本题总分：10分
【问题描述】
在ISO国际标准中定义了A0纸张的大小为1189mm×841mm，将A0纸沿长边对折后为A1纸，大小为841mm×5mm，在对折的过程中长度直接取下整（实际裁剪时可能有损耗）。将A1纸沿长边对折后为A2纸，依此类推。输入纸张的名称，请输出纸张的大小。
【输入格式】
输入一行包含一个字符串表示纸张的名称，该名称一定是A3、A4、A5、A6、A7、A8、A9之一
【输出格式】
输出两行，每行包含一个整数，依次表示长边和短边的长度。
【样例输入1】
A0
【样例输出1】
1189
841
【样例输入2】
A1
【样例输出2】
841
594

line = 1189
col = 841
size = input()
times = int(size[1:])
print(times)
for i in range(times):
    if line >= col: line = line // 2
    else: col = col // 2
print(max([line,col]))
print(min([line,col]))

试题 D: 数位排序

时间限制：1.0s
内存限制：512MB
本题总分：10分
【问题描述】
小蓝对一个数的数位之和很感兴趣，今天他要按照数位之和给数排序。当两个数各个数位之和不同时，将数位和较小的排在前而，当数位之和相等时，将数值小的排在前。例如，2022排在409前面，因为2022的数位之和是6，小于409的数位之和13。
又如，6排在2022前，因为它们的数位之和相同，而6小于2022。
给定正整数n，m，请问对1到n采用这种方法排序时，排在第m个的元素是多少？
【输入格式】
输入第一行包含一个正整数n。第二行包含一个正整数m。
【输出格式】
输出一行包含一个整数，表示答案。
【样例输入】
13
5
【样例输出】
3
【样例说明】
1 到 13 的排序为：1, 10, 2, 11, 3, 12, 4, 13, 5, 6, 7, 8, 9。第 5 个数为 3。
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ m ≤ n ≤ 300。对于 50% 的评测用例，1 ≤ m ≤ n ≤ 1000。对于所有评测用例，1 ≤ m ≤ n ≤ 106。

maxnum = int(input())
pos = int(input())

def summary(num):
    length = len(str(num))
    s = 0
    for i in str(num):
        s += int(i)
    return s
nums = []
for i in range(1,maxnum+1):
    nums.append((i,summary(i)))
nums.sort(key=lambda s: s[0])
nums.sort(key=lambda s: s[1])
print(nums[pos-1][0])

试题 E: 蜂巢

时间限制: 1.0s
内存限制: 512.0MB
本题总分：15 分
【问题描述】
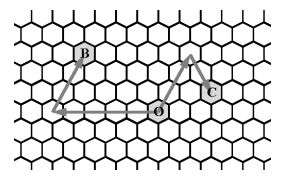
蜂巢由大量的六边形拼接而成，定义蜂巢中的方向为：0 表示正西方向，1表示西偏北 60◦，2 表示东偏北 60◦，3 表示正东，4 表示东偏南 60◦，5 表示西
偏南 60◦。对于给定的一点 O，我们以 O 为原点定义坐标系，如果一个点 A 由 O 点先向 d 方向走 p 步再向 (d + 2) mod 6 方向（d 的顺时针 120◦ 方向）走 q 步到达，则这个点的坐标定义为 (d, p, q)。在蜂窝中，一个点的坐标可能有多种。下图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。

给定点 (d1, p1, q1) 和点 (d2, p2, q2)，请问他们之间最少走多少步可以到达？
【输入格式】
输入一行包含 6 个整数 d1, p1, q1, d2, p2, q2 表示两个点的坐标，相邻两个整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示两点之间最少走多少步可以到达。
【样例输入】
0 5 3 2 3 2
【样例输出】
7
【评测用例规模与约定】
对于 25% 的评测用例，p1, p2 ≤ 103 ；
对于 50% 的评测用例，p1, p2 ≤ 105 ；
对于 75% 的评测用例，p1, p2 ≤ 107 ；
对于所有评测用例，0 ≤ d1, d2 ≤ 5，0 ≤ q1 < p1 ≤ 109，0 ≤ q2 < p2 ≤ 109 。

1	print('没做出来……')

试题 F: 消除游戏

时间限制: 3.0s
内存限制: 512.0MB
本题总分：15 分
【问题描述】在一个字符串 S 中，如果 S i = S i−1 且 S i , S i+1 ，则称 S i 和 S i+1 为边缘字符。如果 S i , S i−1 且 S i = S i+1，则 S i−1 和 S i 也称为边缘字符。其它的字符都不是边缘字符。对于一个给定的串 S，一次操作可以一次性删除该串中的所有边缘字符（操作后可能产生新的边缘字符）。请问经过 2 64 次操作后，字符串 S 变成了怎样的字符串，如果结果为空则输出 EMPTY。
【输入格式】
输入一行包含一个字符串 S 。
【输出格式】
输出一行包含一个字符串表示答案，如果结果为空则输出 EMPTY。
【样例输入 1】
edda
【样例输出 1】
EMPTY
【样例输入 2】
sdfhhhhcvhhxcxnnnnshh
【样例输出 2】
s
【评测用例规模与约定】
对于 25% 的评测用例，|S | ≤ 103 ，其中 |S | 表示 S 的长度；
对于 50% 的评测用例，|S | ≤ 104 ；
对于 75% 的评测用例，|S | ≤ 105 ；
对于所有评测用例，|S | ≤ 106，S 中仅含小写字母。

s = input()
times = 2**64
mark = 'F'*len(s)
nextS = ''
empty = False
NoOperation = True
for time in range(times):
    if s == '':
        empty = True
        break
    for i in range(len(s)):
        if i == (len(s)-1): continue    
        if s[i] == s[i+1] and s[i] != s[i-1]:   # 与右边相同与左边不同
            NoOperation = False
            mark = mark[:i-1] + 'TT' + mark[i+1:]
        elif s[i] == s[i-1] and s[i] != s[i+1]:    # 与左边相同与右边不同
            NoOperation = False
            mark = mark[:i] + 'TT' + mark[i+2:]
    if NoOperation: break
    for i in range(len(mark)):
        if mark[i] == 'F':
            nextS += s[i]
    s = nextS
    nextS = ''
    mark = 'F'*len(s)
    NoOperation = True
if empty:
    print('EMPTY')
else:
    print(s)

试题 G: 全排列的价值

时间限制: 1.0s
内存限制: 512.0MB
本题总分：20 分
【问题描述】
对于一个排列 A = (a1, a2, · · · , an)，定义价值 ci 为 a1 至 ai−1 中小于 ai 的数的个数，即 bi = |{aj | j < i, aj < ai}|。定义 A 的价值为 ∑n i=1 ci。给定 n，求 1 至 n 的全排列中所有排列的价值之和。
【输入格式】
输入一行包含一个整数 n 。
【输出格式】
输出一行包含一个整数表示答案，由于所有排列的价值之和可能很大，请输出这个数除以 998244353 的余数。
【样例输入 1】
3
【样例输出 1】
9
【样例输入 2】
2022
【样例输出 2】
593300958
【样例说明】
1 至 3 构成的所有排列的价值如下:
(1, 2, 3) : 0 + 1 + 2 = 3 ；
(1, 3, 2) : 0 + 1 + 1 = 2 ；
(2, 1, 3) : 0 + 0 + 2 = 2 ；
(2, 3, 1) : 0 + 1 + 0 = 1 ；
(3, 1, 2) : 0 + 0 + 1 = 1 ；
(3, 2, 1) : 0 + 0 + 0 = 0 ；
故总和为 3 + 2 + 2 + 1 + 1 = 9。
【评测用例规模与约定】
对于 40% 的评测用例，n ≤ 20 ；
对于 70% 的评测用例，n ≤ 5000 ；
对于所有评测用例，2 ≤ n ≤ 106 。

这题没做完

from itertools import permutations

n = int(input())
summary = 0

ls = list(range(1,n+1))
MaxPermutations = []
for i in permutations(ls):
    lesscount = 0
    for j in i:
        for k in range(i.index(j),len(i)):
            if j < i[k]: lesscount += 1
    summary += lesscount
mods = summary % 998244353
print(mods)
##    if i[0] == n: MaxPermutations.append(i)
##    else: break
##print(MaxPermutations)

试题 H: 技能升级

时间限制: 1.0s
内存限制: 512.0MB
本题总分：20 分
【问题描述】
小蓝最近正在玩一款 RPG 游戏。他的角色一共有 N 个可以加攻击力的技能。其中第 i 个技能首次升级可以提升 Ai 点攻击力，以后每次升级增加的点数都会减少 Bi。⌈ Ai Bi ⌉ (上取整) 次之后，再升级该技能将不会改变攻击力。现在小蓝可以总计升级 M 次技能，他可以任意选择升级的技能和次数。请你计算小蓝最多可以提高多少点攻击力？
【输入格式】
输入第一行包含两个整数 N 和 M。以下 N 行每行包含两个整数 Ai 和 Bi。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3 6 10 5 9 2 8 1
【样例输出】
47
【评测用例规模与约定】
对于 40% 的评测用例，1 ≤ N, M ≤ 1000；
对于 60% 的评测用例，1 ≤ N ≤ 104 , 1 ≤ M ≤ 107；
对于所有评测用例，1 ≤ N ≤ 105，1 ≤ M ≤ 2 × 109，1 ≤ Ai , Bi ≤ 106。

from math import ceil
TotalATK = 0
SkillCounts, UpgradeTimes = list(map(int, input().split(' ')))
Skills = []
for i in range(SkillCounts):
    ATK, PointMinus = list(map(int, input().split(' ')))
    MaxUpgradeTimes = ceil(ATK/PointMinus)
    Skills.append([ATK, PointMinus, MaxUpgradeTimes])

Skills.sort(key=lambda s: s[0],reverse=True)

for i in range(UpgradeTimes):
    TotalATK += Skills[0][0]
    Skills[0][0] -= Skills[0][1]    # ATK减少固定值
    Skills[0][2] -= 1   # 可升级次数-1
    Skills.sort(key=lambda s: s[0],reverse=True)
print(TotalATK)

试题 I: 最长不下降子序列

时间限制: 1.0s
内存限制: 512.0MB
本题总分：25 分
【问题描述】
给定一个长度为 N 的整数序列：A1, A2, · · · , AN。现在你有一次机会，将其中连续的 K 个数修改成任意一个相同值。请你计算如何修改可以使修改后的数列的最长不下降子序列最长，请输出这个最长的长度。最长不下降子序列是指序列中的一个子序列，子序列中的每个数不小于在它之前的数。
【输入格式】
输入第一行包含两个整数 N 和 K。第二行包含 N 个整数 A1, A2, · · · , AN。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
5 1 1 4 2 8 5
【样例输出】
4
【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ K ≤ N ≤ 100；
对于 30% 的评测用例，1 ≤ K ≤ N ≤ 1000；
对于 50% 的评测用例，1 ≤ K ≤ N ≤ 10000；
对于所有评测用例，1 ≤ K ≤ N ≤ 10^5，1 ≤ Ai ≤ 10^6。

好像我的做法有点bug？

Counts, Constant = list(map(int, input().split()))
Array = list(map(int, input().split()))
SubCount = []
# 前面的往小了改的话就得改成0，后面的往大了改就可以改很大

Min = []
Max = []

for i in range(len(Array)):
    Min.append(min(Array[i:]))
    try:
        Max.append(max(Array[:i]))
    except ValueError:      # 第一个数字前面没有数字
        Max.append(0)

for i in range(len(Min)):
    if i == len(Min)-1: break
    Count = 0 
    for j in Min[i+1:]:
        if j >= Min[i]: Count += 1
        else: break
    SubCount.append(Count)
MaxSubCount = max(SubCount)     # 获取当前最长子序列的位置
if SubCount.index(MaxSubCount)+1 <= Constant:
    Result = SubCount.index(MaxSubCount) + MaxSubCount
else:
    Result = MaxSubCount + Constant
print(Result)

试题 J: 最优清零方案

时间限制: 5.0s
内存限制: 512.0MB
本题总分：25 分
【问题描述】
给定一个长度为 N 的数列 A1, A2, · · · , AN。现在小蓝想通过若干次操作将这个数列中每个数字清零。每次操作小蓝可以选择以下两种之一： 1. 选择一个大于 0 的整数，将它减去 1； 2. 选择连续 K 个大于 0 的整数，将它们各减去 1。小蓝最少经过几次操作可以将整个数列清零？
【输入格式】
输入第一行包含两个整数 N 和 K。第二行包含 N 个整数 A1, A2, · · · , AN。
【输出格式】
输出一个整数表示答案。
【样例输入】
4 2 1 2 3 4
【样例输出】
6
【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ K ≤ N ≤ 10。
对于 40% 的评测用例，1 ≤ K ≤ N ≤ 100。
对于 50% 的评测用例，1 ≤ K ≤ N ≤ 1000。
对于 60% 的评测用例，1 ≤ K ≤ N ≤ 10000。
对于 70% 的评测用例，1 ≤ K ≤ N ≤ 100000。
对于所有评测用例，1 ≤ K ≤ N ≤ 1000000, 0 ≤ Ai ≤ 1000000。

印象中这题没做完？

Length, Constant = list(map(int, input().split(' ')))   # 获得数列长度以及连续的数字的数量K
Array = list(map(int, input().split(' ')))  # 构造输入的数列
MinusTimes = []

##def GetConstantArray(array):
##    ConstantPosList = []
##    for i in range(len(array)):
##        if i == len(array)-1: break
##        if array[i]+1 == array[i]:
##            StartPos = i
##            CusPos = i+1
##            EndPos = i+1
##            while 1:
##                if CurPos+1 >= len(array):        # 指针已经指向最后一个数字了
##                    ConstantPosList.append((StartPos, EndPos))      # 将位置信息存储进入列表中，终止循环
##                    break                    
##                if array[CurPos+1] == array[CurPos]+1: CurPos += 1      # 当指针指向的下一个数字与当前指向的数字+1相等就继续
##                else:   # 指针指向的下一个数字与当前数字+1不相等
##                    ConstantPosList.append((StartPos, EndPos))      # 将位置信息存储进入列表中，终止循环
##                    break
##    return ConstantPosList
##print(GetConstantArray(Array))

for i in range(Length):
    if i+Constant >= Length+1: break
    MinusTimes.append(max(Array[i:i+Constant]))

MaxMinusTimes = max(MinusTimes)
MaxMinusTimesPos = MinusTimes.index(MaxMinusTimes)
MinusTimesSum = []
for i in range(Constant):
    try:
        MinusTimesSum.append(sum(MinusTimes[MaxMinusTimesPos-i:MaxMinusTimes+i]))
    except:
        MinusTimesSum.append(sum(MinusTimes[MaxMinusTimesPos-i:]))
MaxMinusTimesSumPos = MinusTimesSum.index(max(MinusTimesSum))    # 确定从哪里开始减，怎么减